APPLIED PHYSCIAL OCEANOGRAPHY
Acoustic-gravity waves (AGW) can be a major player in producing currents at various water depths. The velocity drift and random flow trajectories induced by AGW are essential for plankton, algae, bacteria, microorganisms and other marine animals that inhabit the pelagic zone: (1) small drifting microorganisms that cannot swim against a current become exposed to larger areas, which enhances their chances of finding food; (2) larger marine animals benefit from the continuous transportation of salt, carbons, nutrients and other substances that drift with the flow. In particular, this is important for sessile animals, e.g. carnivorous sponges, that live in the deep ocean reaching more than 8000 m.
In principle, the simultaneous generation of many AGW, say along a continental shelf, may result in relatively large currents with volumetric flow rates reaching few to tens of Sverdrups, that are comparable to global surface and deep currents. Identifying regions of high probability for the generation of AGW from various sources, i.e. wave-wave interactions, tectonic movements, etc., is essential for quantifying the local and global contribution of AGW, a work that requires future multidisciplinary collaborations.

The effect of the compressibility of the ocean and its role in generating progressive compression-type waves (acoustic-gravity waves) are revisited. Originally, Longuet-Higgins (1950) obtained a solution for the nonlinear interaction of two opposite waves in a compressible fluid, which results in the generation of compression waves. In this work we extend this solution to include the general interaction of waves of profoundly different wavelengths. We also fully solve the special triad resonance case obtained by Longuet-Higgins (1950).

The nonlinear triad-interaction of two opposing gravity waves with almost identical frequencies and one much longer acoustic-gravity wave is studied for non-resonance, as well as for exact resonance conditions. For non-resonance conditions the previously known results for a `bound' acoustic-gravity wave are recovered. For resonance, or near-resonance conditions, where all three waves are `free-waves', the interaction is recurrent and the amplitude of the free acoustic-gravity wave turns out to be much larger than that known for the bound wave. The results for the recurrent evolution are given analytically, in terms of Jacobian elliptic functions and elliptic integrals.
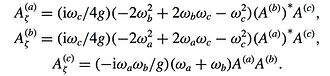
Evolution equations:
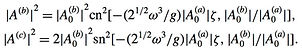
Solution for the Longuet-Higgins case:
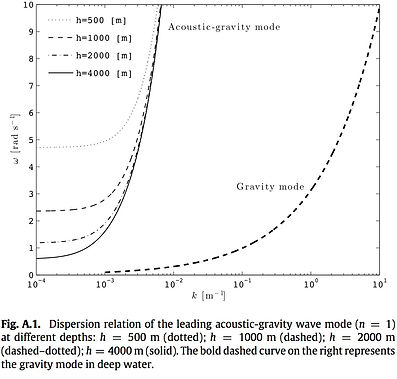
The mathematical solution for the two-dimensional linear problem of acoustic-gravity waves in a compressible ocean with an elastic bottom is presented. The physical properties of these waves are studied, and compared with those for waves over rigid ground. The solutions for constant water depth, together with the assumption of constant energy flux, are used to study the shoaling of acoustic-gravity waves over a slowly-varying bathymetry. The present work enriches our knowledge about acoustic-gravity waves in a way that could assist, among others, in the early detection of tsunami.

Fig. 1. Schematic representation of the flow domain; h is the water depth; η(x, t ) is the surface elevation; φl is the velocity potential of the liquid medium; φs and ψs are the dilatation and rotation potentials of the half-space solid medium, respectively.
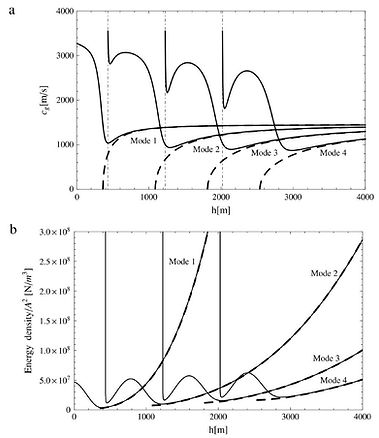
Fig. 5. Progressive acoustic-gravity modes with the frequency 1 Hz. Variation with depth of: (a) the group velocity; and (b) the ratio of the energy density to the square of the free-surface-amplitude. Dashed curves: rigid bottom; solid curves: elastic bottom.
A mathematical solution of the two-dimensional linear problem of an acoustic-gravity wave propagating over a bottom with a step, in a slightly compressible ocean, is presented. Expressions for the flow field on both sides of the step are derived. Furthermore, an extended problem is given that provides a solution for a group of acoustic-gravity waves, generated by a submarine earthquake, propagating toward a continental shelf. The dynamic bottom pressure produced by the acoustic-gravity waves is probably measurable, especially at the vicinity of the seaward face of the shelf break where incident and reflected modes appear simultaneously. A successful recording of such bottom pressures could assist in the early detection of tsunami.

A mathematical solution of the two dimensional linear problem of an acoustic–gravity wave propagating over a rigid and slowly-varying bathymetry, in an acoustically homogeneous and slightly compressible ocean, is presented. Expressions for the far and near flow fields are derived. The present note enriches our knowledge about acoustic–gravity waves in a way that could assist, among others, in the early detection of tsunami.
Figure. Envelope of the far field solution (dashed–line) for the dynamic bottom pressure am- plification factor AF as function of frequency f = ω/2π, at a constant depth h0 = 250 m. Local seabed slope s0 = 0.001. Ocean depth is hL = 4000 m.
